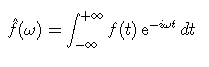
The Fourier transform analyses the "frequency contents" of a signal.
Its many properties make it suitable for studying linear time invariant operators, such as differentiation.
It is a global representation of a signal.
The Fourier transform of f in L2 is
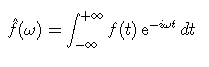
The inverse Fourier transform represents f as a sum of sinusoids
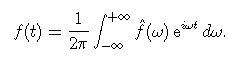
The Fourier transform has many algebraic properties. Note that sinusoidal waves are eigenvectors of the differentiation operator.
This makes it possible for the Fourier transform to give indications on the regularity of a signal.
To reduce the number of operations, the Fast Fourier Transform separates odd and even frequencies when computing a discrete Fourier transform.
The Fourier transform is a global representation of the signal. It cannot analyze it local frequency contents or its local regularity. The convergence condition on the Fourier transform only gives the worst order of regularity. It ignores local regular behaviours.
There exist, however, a definition of the instantaneous frequency of an analytic signal.
It is useless in practice because it fails to detect the summation of two signals. It is nonetheless a convenient means of defining synthetic signals for numerical experimentations.
Trying to discriminate each of the stacked frequencies leads to a frequency analysis that is localized in frequency as well as in time. This requires some understanding of the time-frequency localization of signal.