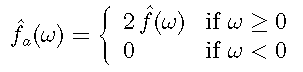
A signal in L2 is analytic if its Fourier transform is zero for negative frequencies. The analytic part fa of a real signal f is given by its Fourier transform:
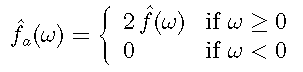
and fa can properly be decomposed into a module and a complex phase:
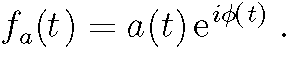
The instantanneous frequency is the nonnegative derivative of the complex phase:
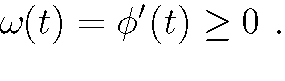
For a sinusoidal wave, this definition coincides with the usual frequency. Unfortunately, the instantaneous frequency of the sum of two ordinary sinusoidal waves is the average of their frequencies, which does not coincide with the result of a Fourier analysis.
Hence the caracterization of the instaneous frequency of a signal in a sense that is consistent with the Fourier analysis in simple cases requires other mathematical tools.
However, analytic signals are very useful in the synthesis of signals with a given time varying frequency contents.