The discrete Fourier transform of a discrete signal with N samples is
Using this formula to compute the Fourier transform requires N2 complex additions and multiplications.
A simple computation shows that the even frequency coefficients are the coefficients of the Fourier transform of the N/2 periodic signal
and that the odd frequency coefficients are the coefficients of the Fourier transform of
One verifies by induction that the number of operations required by this method to compute the Fourier transform is of the order of KN log2(N), where K is a constant which does not depend on N.
This is the basic principle of the Fast Fourier Transform. Variants exist that reduce K.
The circular convolution of two N periodic signals is defined by
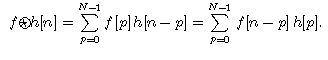
The discrete Fourier transform of a circular convolution is the product of the two discrete Fourier transforms.
For two signals f and h with a length M>=32, computing their convolution with an FFT is faster than using the straightforward formula. For that purpose, two M periodic signals are defined:
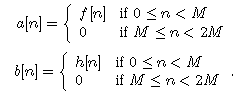
and one can verify that their circular convolution is equal to the convolution
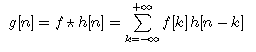
for 0<=n<2M. The circular convolution is itself computed by performing the FFT of the two signals, computing their product and then its inverse FFT.