There is no finite energy function which is compactly supported both in the time and frequency domains.
The time-frequency localization is measured in the mean squares sense and is represented as a Heisenberg box.
The Fourier transform can be viewed as a representation of a function as a sum of sinusoidal waves. These sinusoids are very well localized in the frequency, but not in time, since their support has an infinite length. This is a consequence of periodicity.
To represent the frequency behavior of a signal locally in time, the signal should be analyzed by functions which are localized both in time and frequency, for instance, signals that are compactly supported in the time and Fourier domains.
This time-frequency localization is limited by the following two results:
If f is in L2, then its time root deviation ![]() and its Fourier root deviation
and its Fourier root deviation ![]() are defined.
Then
are defined.
Then
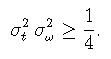
A balance has to be reached between the time and
frequency resolution. In the limit case of a sinusoid,![]() is zero and
is zero and ![]() is
infinite.
is
infinite.
The previous inequality is an equality if and only if f is a Gabor chirp .
If f is non zero with a compact support, then its Fourier transform cannot be zero on a whole interval. Similarly, if its Fourier transform is compactly supported, then it cannot be zero on a time interval.
Hence, even if the Heisenberg constraints are verified, it is impossible to have an function in L2 which is compactly supported both in the time and Fourier domains.
In particular, this means that there is no instantaneous frequency analysis for finite energy signals.
This localization is represented as a Heisenberg box.
For a family of vectors to be a basis of L2, it is reasonable to expect that their Heisenberg boxes pave the time frequency plane.
Two time frequency localization strategies are presented in parallel; the first one leads to the windowed Fourier transform, while the other one leads to the wavelet transform.