Orthogonal Wavelets

Let us recall that a multiresolution approximation is a nested sequence of linear spaces. The orthogonal complement W_j of V_j in V_j-1 can be thus defined:

Then there is a function y such that the family y_j,n(t) = 2^-j/2 y(2^-jt-n), n in Z, is an orthonormal basis of W_j. The family y_j,n, j in Z and n in Z, is an orthonormal basis of L² and

y is an orthogonal wavelet associated to the multiresolution approximation. A signal f in L² can be decomposed as

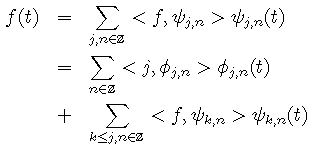
where f is an orthogonal scaling function of the multiresolution.

A theorem by Mallat and Meyer builds an orthogonal wavelet from a scaling function.

Example

Here is a cubic spline scaling function and the corresponding cubic spline Battle-Lemarié wavelet, and their Fourier transform. The wavelet is a cubic spline because it is a linear combination of cubic splines.

The wavelet is not compactly supported.

From the real axis to the interval

Wavelet bases are bases of L²(R). There are several methods to transform them into wavelet bases over an interval. Once discretized, they are used to process finite signals.

From dimension 1 to dimension 2

There are several methods to build wavelet bases on functional spaces in dimension greater than 1. The simplest ones uses separable wavelets.

Properties