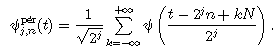
Until now, only wavelets over the real axis have been considered, e.g. wavelets that are suited to the analysis of signals defined over the whole axis. In most cases, signals are compactly supported; images, in particular, are explicitely defined over a rectangle of pixels.
The wavelets considered here are compactly supported.
A [0,N] supported signal can be represented as the product of a general signal with the caracteristic function of [0,N]. The discontinuities of this function require special attention. Three methods are known to handle them, the last one being the most efficient.
The wavelets are periodized by the following transformation:
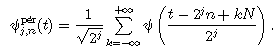
with j<=log2N. This is equivalent to a signal periodization.
Wavelets which are completely inside the interval are not changed. Wavelets that ovelap the boudaries are cut into two pieces loacated at the left and right edges of the interval. Separately, each of the pieces have no vanishing moment. This creates large wavelet coefficients when the periodized signal is not itself continuous.
To bypass this problem, the signal is symmetrically folded around the right edge of the interval and periodized over the double sized interval.
This yields a continuous periodic signal.
Porting the signal transformation to the wavelet basis shows that the vector family is a basis of L2[0,N] if the wavelet is symmetric or antisymmetric. This puts orthogonal bases asides.
In fact, the continuity problem reappears at the next derivative. The following approach takes the problem at the root, which is how to make wavelets over an interval with vanishing moments.
Boundary effects are explicitely handled. Consider an Daubechies orthogonal basis with p vanishing moments.
From the Strang et Fix conditions, it appears that there exists a polynomial qk of degree k such that:
for k<p.
This equation is multiplied by the caracteristic function of [0,N]. Assuming that the support of j is [-p+1,p], scaling functions with indices p<=k<N-p are not changed by this restriction. To recover the Strang and Fix condition on the interval, p "left" edge scaling function and p "right" edge scaling functions are to be found such that
If this equation is satisfied, it reamains valid after rescaling since the nk, up to a power of 2, are the scaling coefficients of qk at all resolutions. There remains to find the filters h and H which satisfy the scaling equation:
where 
denotes
the whole set of scaling functions obtained by translation at the
resolution j, and to verify the orthogonality condition.
The coefficients of these filters are available in Wavelab, using the function MakeCDJVFilter.