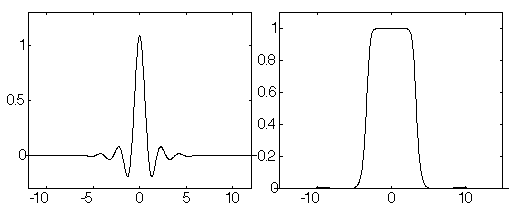
The Riesz basis can be transformed into an orthogonal basis generated by integer translations of an elementary function, which is called a scaling function. It is a particular case of a biorthogonal system where both bases are equal.

One can verify that the other resolutions are generated by a suitable dilatation of these bases of translated atoms. Since the resolutions are embedded, there is necessarily a sequence of real numbers h[n] such that
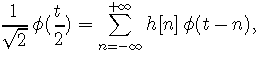
or, in the Fourier domain
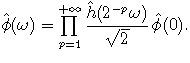
assuming the Fourier transform is continuous.
It is proved that h is a conjugate mirror filter. It entirely determines the scaling function and most of its properties. In particular, the scaling function is compactly supported if and only if h has a finite number of non zero coefficients. h is sais to be a Finite Impulse Response (FIR) filter. For more info, see the page on the properties of of orthogonal wavelets and how they are related the the filter h.
As an example, the filter coefficients that correspond to the cubic spline scaling function are given.
The study of the filters h which generate multiresolution approximations has produced many important theorems. The following one gives necessary and sufficient conditions for h to generate a scaling function:
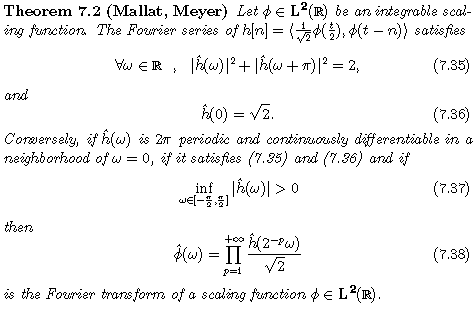
Condition (7.35) means that h is a conjugate mirror filter. Condition (7.36) is simply a normalization. Condition (7.37) garantees that the function defined by (7.38) has a finte energy.
The scaling equations shows that the scaling coefficients a1 [n] = < a , j(t/2-n) > of a in V1 are obtained from the scaling coefficients a0 [n] = < a , j(t-n) > in V0 by a convolution with the conjugate mirror filter h and a subsampling:
Back to Multiresolution Approximations