The fast dyadic wavelet transform is implemented using filter banks. This implementation is very close to the implementation of the fast (bi)orthogonal wavelet transform, except that no subsampling is performed.
For any j>=0, let
and the discrete data is likened to the a0[n]. We also define
For a given filter x with coefficients
x[n], xj[n] denotes the filter obtained by
inserting 2j-1 zeroes between every x coefficient (hence
the French name "algorithme à trous", which means "holes
algorithm"), and let ![]()
The algorithme à trous computes the fast dyadic wavelet transform in the following way:
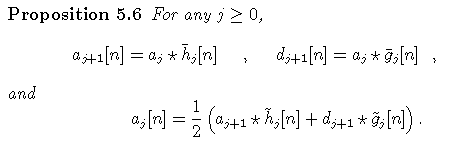
(the ~ filters are the dual filters of the biorthogonal system).
Compare this algorithm to the decomposition and reconstruction algorithm over a basis of biorthogonal wavelets. In the decomposition case, the data is convolved with the symmetrized filter, then the output is subsampled. Here the filter is "stretched" to take into account the rescaling and the convolution is performed without any subsampling.
Here is a scheme of the filter bank:

Reconstruction From Dyadic Maxima