
The scaling equations on the scaling functions and wavelets show that the decomposition and reconstruction of a signal from a resolution to the next one is implemented by perfect reconstruction filter banks.
The scaling equations imply the coefficients a1 [n] and d1 [n] of a signal in Vj and Wj are computed from its coefficients a0[n] in Vj-1 by applying the filters h and g and subsampling the output:
with h1[n] = h[-n] and g1[n] = g[-n].

In practice this recursion is initialized by considering that the discrete signal samples are some fine resolution coefficients.
The coefficients of h and g are defined by the scaling equations
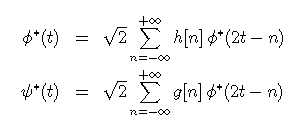
or, in the Fourier domain:
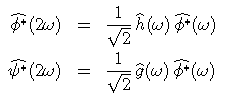
Conversely, a0[n] is reconstructed from a1 [n] and d1 [n] by inserting zeroes between two consecutive samples and summing their convolutions with the dual filters h2 et g2 which define the dual scaling equations:
where the z operator represents the insertion of zeroes.
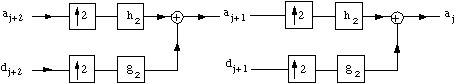
The coefficients of h2 and g2 are defined by the scaling equations
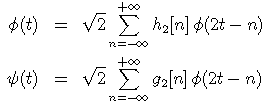
or, in the Fourier domain:
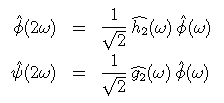
This algorithm is used to evaluate the scaling functions and wavelets. Indeed the coefficients of a scaling function (resp. wavelet) are all zero but for one within their on resolution (resp. detail) space basis. The reconstruction algorithm provides the coefficients in the finer resolutions. For high resolutions, the scaling coefficients are considered to be samples of the function.
Hence the construction of biorthogonal wavelets is equivalent to the synthesis of perfect reconstruction filters having a stability property.