The Fourier transform analyses the global regularity of a function.
The wavelet transform makes it possible to analyze the pointwise regularity of a function.
A signal is regular if it can be locally approximated by a polynomial. The definition of the Lipschitz regularity is
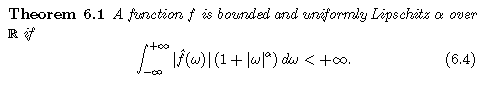
Naturally, this a global regularity condition.
To get conditions on the local or even pointwise regularity of a signal, it is necessary to use a transform which is localized in time.
Assume that the wavelet has n vanishing moments:
and has n continuous derivatives with a fast decay.
A fast decaying wavelet has n vanishing moments if and only if its is the nth derivative of a fast decaying function.
If f is a function which is a little bit more than n times differentiable at point v, then it can be approximated by a polynomial of degree n. The wavelet transform of this polynomial is zero; around v, its order is that of the error between the polynomial and the function. If this error can be uniformly estimated on an interval, this yields a tool for regularity analysis on an interval.
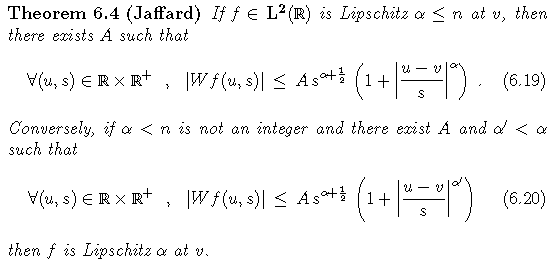
This condition relates the pointwise regularity of a signal to the decay of its wavelet transform's modulus.
It can be extended to an interval and, of course, to the whole real axis.