Wavelet transform modulus maxima are related to the singularities of the signal.
More precisely, the following theorem proves that there cannot be a singularity without a local maximum of the wavelet transform at the finer scales.
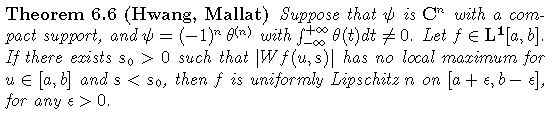
This theorem indicates the presence of a maximum at the finer scales where a singularity occurs. In the general case, is sequence of modulus maxima is detected which converges to the singularity. Below are the modulus maxima of the previous example:
Warning: these are the modulus maxima of the wavelet transform. Instantanuous frequencies are detected from the maxima of the normalized scalogram:
![]() which
differs in two ways: normalization, and the fact that the variable is
homogeneous to a frequency, and not to a scale.
which
differs in two ways: normalization, and the fact that the variable is
homogeneous to a frequency, and not to a scale.
When the wavelet is the nth derivative of a gaussian, the maxima curves are connected and go through all of the finer scales.
The decay rate of the maxima along the curves indicate the order of the isolated singularities (this a consequence of theorems 6.4 et 6.6 when extended to an interval):
The modulus maxima are displayed as a function of the scale in log-log axes, and the slope gives the estimated singularity order. Below is such a curve for two singularities: the solid line corresponds to the singularity at t=14 and the dotted line to the singularity at t=108. Fine scales are on the left.
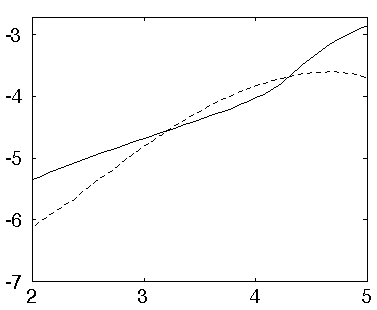
For t=14, the slope is 1/2, and the signal is 0-Lipschitz here, that is, it has a discontinuity. For t=108, the slope is close to 1, which indicates that the signal is 1/2 Lipschitz here.