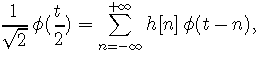
When the Riesz basis is an orthogonal basis, the multiresolution approximation is orthogonal, and the base atom is called a scaling function. It is always possible to orthogonalize a multiresolution approximation.
However, orthogonalities imposes some constraints that may not be desirable. One of the most important is that a compactly supported (orthogonal) scaling function cannot symmetric and continuous. The symmetry is useful in the analysis of finite signals.
Some of these restrictions (notably the absence of symmetry) can be avoided by using biorthogonal multiresolution approximations.
The "approximation" denomination means that an orthogonal or biorthogonal multiresolution analysis (or approximation) can be related to a sequence of respectively orthogonal or oblique projectors, which efficiently approximate regular signals. The order of approximation is determined by the degree of the polynomials that can be reconstructed in the resolutions.
Multiresolution approximations are determined by one or two atoms f which generate respectively the orthogonal or biorthogonal multiresolutions.
By definition of a multiresolution, f(t/2) is a linear combination of the f(t-n). This relation is called a scaling equation:
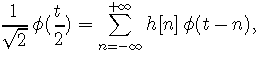
In the Fourier domain, this becomes
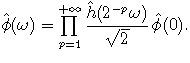
The coefficients h[n] in the scaling equation entirely determine f, and finding them is equivalent to the design of a filter bank, plus some stability conditions to be able to generate L2.
As the scale j gets finer the approximations becomes more accurate (see Lena). Switching from the resolution j to j-1 adds details to the signal. The same way that approximations can be decomposed on resolution bases, these extra details can be decomposed in detail bases.
Details bases, like resolution bases, ore obtained by translating a single resealed atom. This atom is called a wavelet. The order of approximation of the multiresolution is equal to the number of vanishing moments of the wavelet. It also represents the wavelet's ability to detect the isolated singularities of a signal.