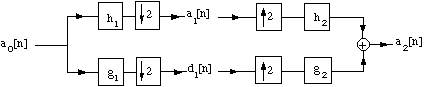
A perfect reconstruction filter bank decomposes a signal by filtering and subsampling.
It reconstructs it by inserting zeroes, filtering and summation.
A (discrete) two-channel multirate filter bank convolves a signal a0 with a low-pass filter h1[n] = h[-n] and a high-pass filter g1[n] = g[-n] and then subsamples the output:
A reconstructed signal a2 is obtained by filtering the zero expanded signals with a dual low-pass filter h2 and a dual high-pass filter g2. If z(x) denotes the signal obtained from x by inserting a zero between every sample, this can be written as:
The following figure illustrates the decomposition and reconstruction process.

The filter bank is said to be a perfect reconstruction filter bank when a2 = a0 . If, additionally, h = h2 and g = g2, the filters are called conjugate mirror filters.
Perfect reconstruction filter banks are caracterized in a theorem by Vetterli. When the filters have a finite impulse response, the g and g2 filters can easily be derived from the h and h2 filters, and the filter synthesis is equivalent to solving
where h and h2 are trigonometric polynomials.