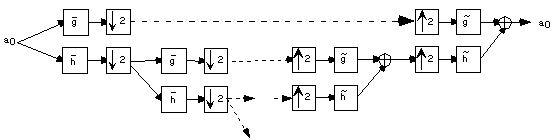
Biorthogonal wavelets and scaling functions are caracterized by a perfect reconstruction filter bank; orthogonal wavelets and scaling functions are caracterized by a pair of conjugate mirror filters. Nonetheless, a perfect reconstruction filter bank (or any pair of conjugate mirror filters) does not necessarily generate a wavelet system. Indeed, some attention has to be paid to the stability of the decomposition and reconstruction schemes as the number of scales increases, that is when the number of filter bank cascades goes to the infinity. This is expressed by an additional condition (7.37) on the conjugate mirror filter h for it to define a scaling function.
The decomposition can be performed on the signal a1 to generate a signal a2 and a signal d2; repeating this construction produces a low resolution signal aj and a sequence of detail signals d1 .... dj.

A recursive decomposition which similar to the previous one can be performed by the algorithme à trous to generate low resolution signal Aj and a sequence of detail signals D1 .... Dj. The two decompositions are related by the following equations:
In the Fourier domain, the transfer between a0 and Aj is
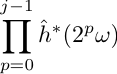
Let us operate a time rescaling T = 2-jt so that the interval between the non zero coefficients of the slower filter is always one. Then the interval between the non zero coefficients of the tightest filter is 2-j. The transfer becomes
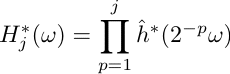
Let j go to the infinity. If the previous transfer
converges in L2, the limit can be interpreted as the Fourier transform of the mirror of a function  , and the processed signal can be written as
, and the processed signal can be written as
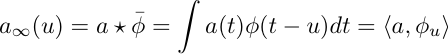
which can be interpreted as the scalar product between the original signal and a translate of the scaling function 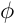 whose Fourier transform is
whose Fourier transform is
The scaling function necessarily satisfies a scaling equation:
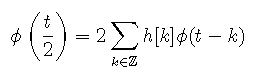
Such functions are at the core of multiresolution analysis, which is itself the sarting point for the definition of dyadic wavelets.