of vectors in a
Hilbert space H is a frame of H if there are two constants A>0 and
B>0 such that, for any f in H,Frames are a stable, possibly redundant, representation of signals.
It is a generalization of the concept of basis in a linear space.
A frame is a family of vectors which can represent any finite energy signal by the sequence of its inner products with the vectors of the family. However, it may be possible that not all sequences of reals represent an finite energy signal. Oversampling is an example of a represention of signals in a frame. One can see that not all sequences of values may represent a sequence of samples. In general, frames are a stable and redundant representation of signals.
A family of vectors in a
Hilbert space H is a frame of H if there are two constants A>0 and
B>0 such that, for any f in H,
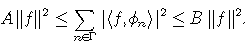
If A=B, the frame is said to be tight.
A Riesz basis is a frame whose vectors are linearly independant.
Example: consider a family of three vectors in the plane which are obtained by succesive rotations of a third of turn of one vector. This family is a tight frame of the plane, with A=B=3/2.
The frame vectors are supposed to be of unit norm.
If the frame vectors are independent, then A<=1<=B. The frame is then an orthonormal basis if and only if A=B=1. If A>1, then the frame is redundant. A finite family is always a frame of the linear space that it generates.
U denotes the operateur which transforms a signal f into the sequence of its frame inner products.
U has one or an infinity of left inverses.
The pseudo-inverse 
of U is the left inverse of U
which is zero on the orthogonal complement of the image of U. It is
the minimum norm left inverse.
It is used to build a signal approximation from any sequence of real numbers. The computation of (U*U)-1f can be performed by a conjugate gradient algorithm.
The image of the frame through (U*U)-1 is a frame called
the dual frame.
For any f in H,
and
If the original frame is a Riesz basis, then the two frames form a biorthogonal basis system, that is
