
L'analyse de Fourier permet de caractériser la régularité globale d'une fonction.
La transformée en ondelettes permet d'analyser la régularité ponctuelle d'une fonction.
Un signal est régulier si on peut l'approximer localement par un polynôme. On donne ici la définition de la régularité Lipschitzienne:

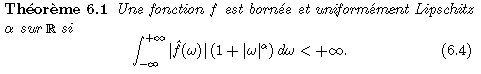
Il s'agit naturellement d'une condition de régularité globale.
Pour obtenir des conditions de régularité localisées ou même ponctuelle, il faut utiliser des transformées localisées en temps.
On suppose que l'ondelette utilisée a n moments nuls:
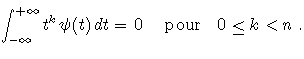
et est n fois dérivables avec des dérivées à décroissance rapide.
Une ondelette à décroissance rapide a n moments nuls si et seulement elle est la dérivée nèmes d'une fonction à décroissance rapide.
Si f est une fonction un peu plus que n fois différentiable en un point v, on peut l'approximer par un polynôme de degré n. La transformée en ondelettes de ce polynôme est nulle; autour de v, elle est donc de l'ordre de l'erreur entre le polynôme et la fonction. Si cette erreur peut être estimée uniformément sur un intervalle, on obtient un outil d'étude de la régularité sur l'intervalle.
Cette condition établit un lien entre la régularité ponctuelle d'un signal et la décroissance du module de sa transformée en ondelettes.
Elle peut être étendue à tout un intervalle, et bien sûr à l'axe réel.